සමහර වැදගත් තේමාවන් විද්‍යාව, ගණිතය සහ තාක්ෂණය පුරාවට ව්‍යාප්තව පවතින අතර අප සලකා බලන්නේ පුරාණ ශිෂ්ටාචාරයන් වේවා,  මනුෂ්‍ය ශරීරය වේවා, එසේත් නැතිනම් ධූම කේතුවක් වේවා  ඒ සෑම තැනකදීම ඒවා යළි යළිත් අපට හමුවෙයි. ඒවා, ශාස්ත්‍රීය ශික්ෂණයන්ගේ මායිම් අභිබවා යන එමෙන්ම සිද්ධාන්තයන්, නිරීක්ෂණ සහ සැලසුම් පැහැදිලි කිරීමේදී ඵලදායි බව  සනාථ වන අදහස්ය. එකී අදහස් කිහිපයක් ගැන මෙන්ම ඒවා විද්‍යාවට, ගණිතය සහ තාක්ෂණය කෙරෙහි කෙසේ යොදාගන්නේ ද යන්න පිළිබඳ නිර්දේශ ද මේ ලිපි පෙළ මගින් ඉදිරිපත් කෙරේ. මේවා පද්ධති, මොඩල,  ස්ථායි බව හා විපර්යාස සහ පරිමාණය යන මාතෘකා ඔස්සේ ඉදිරි සඳුදා දිනවල තතු ඔබට ගෙන එනු ඇත

ගණිතමය අනුකෘති

ගණිතමය අනුකෘති කරණයෙහි මූලික අරමුණ වනුයේ අප උනන්දුවක් දක්වන පද්ධතියක් ක්‍රියා කරන ආකාරයටම හැසිරෙන ගණිතමය සම්බන්ධතාවන් සොයා ගැනීමයි.  (මෙහි දී  පද්ධතිය යනු වෙනත් වියුක්තිකරණයන් (abstractions) මෙන් ම භෞතික හා ජීව විද්‍යාත්මක සංසිද්ධි විය හැකියි.  නිදසුනක් දක්වන්නේ නම් පහළට වැටෙන ගලක (පාෂාණයක) වර්ධනය වන වේගය,  v = gt යනුවෙන්   සංකේතාත්මක සම්බන්ධතාවක් ලෙස දැක්විය හැකි වේ. මෙම සමීකරණයේ g සඳහා අචල අගයක් ඇත. මෙම අනුකෘතිය හඟවන්නේ පහළ වැටීමේ වේගය (v) පහළ වැටීම සඳහා වැය වන කාලයට අනුපාතිකව (t) වැඩිවන බවයි.

ගණිතමය අනුකෘතියක් යම් සංසිද්ධියක් ඒවා දැනටමත් නිරීක්ෂණය කරනු ලැබූ අවස්ථාවෙන් පරිබාහිරව කෙබඳු වේදැයි යන්න පුරෝකථනය කිරීමට මගපාදයි හැබැයි ඒ ඒවා කෙබඳු වේදැයි යන්නපමණකි. බොහෝවිට, (උෂ්ණත්වය හෝ වේලාව වැනි) තත්ත්වයන් කුඩා පරාසයක් තුළ ඇතිවන සංසිද්ධිවලට ගැලපෙන ගණිතමය අනුභූතියක් සපයාගැනීම සැලකිය යුතු දුරකට පහසුයි. එහෙත් පුළුල් පරාසයක දී එය නොගැලපීමට ඉඩ තිබේ. v = gt යන්න (නිශ්චලව තිබී) මීටර කිහිපයක් දුරක්   පහළට වැටෙන පාෂාණයක් වැනි වස්තුවක් සම්බන්ධයෙන් නිවැරදිව යොදාගත හැකි වුවත්, (වාතය එහි රෝධය හෙවත් ඇදීම එහි වේගය සීමා කරන හෙයින්) වස්තුව  පත්‍රයක් නම් ද එමෙන්ම පතිත වීම ඉතාමත් විශාල දුරක් තුළ නම් ද (රෝධය වැඩිවන විට ආකර්ෂණයේ බලය වෙනස් වෙයි) එය සංසිද්ධිය හා මනාව නොගැලපේ.

අංක ගණිතමය වේවා, තර්ක ශාස්ත්‍රීය හෝ ජ්‍යාමිත්‍යමය වේවා ගතයුතු පියවර මාලාවක්  යථාතථ්‍යව  විදහා දක්වන නිති රීති හා උපදෙස් පෙළක් අනුකෘති අතරට ඇතුළත් විය හැකිය. සමහර අවස්ථාවල ඉතාමත් සරල නීති රීති හා උපදෙස්  වුව ද  ඇත්තවශයෙන්ම අනුගමනය කරනු ලැබ විනා ඒවායේ ප්‍රතිවිපාක පුරෝකතනය කිරීම අතිශය දුෂ්කර විය හැකිය. ඉතා දීර්ඝ හෝ සංකීර්ණ උපදෙස් ක්‍රියාවට නැංවීමේ දී ඒවායේ ප්‍රතිවිපාක කවරේ දැයි ගවේෂනය කිරීමට අධිවේගී පරගණකවලට පුළුවන. නිදසුනක් ගනිමු. න්‍යෂ්ඨික බලාගාරයක් එහි පාලන පද්ධතිය සෑම කොටසකම අනාවරක (detectors) සහ අනතුරු හැඟවීමේ සංඥා ඇති ආකාරයට සැලසුම් කළ හැකි වුවද විවිධ වූ සංකීර්ණ අවස්ථාවක් යටතේ කුමක් සිදුවේදැයි පුරෝකතනය කිරීම අසීරුය. ඇණහිටීමේ විවිධ තත්ත්වයන් යටතේ පද්ධතිය ක්‍රියාකාරී වන්නේ කොයි ආකාරයටද යන්න විඩම්බනය පිණිස (simulate) පාලන පද්ධතියේ සෑම කොටසක් සඳහා වූ ගණිතමය ආකෘති එකිනෙකට සම්බන්ධ කළ හැකිය.

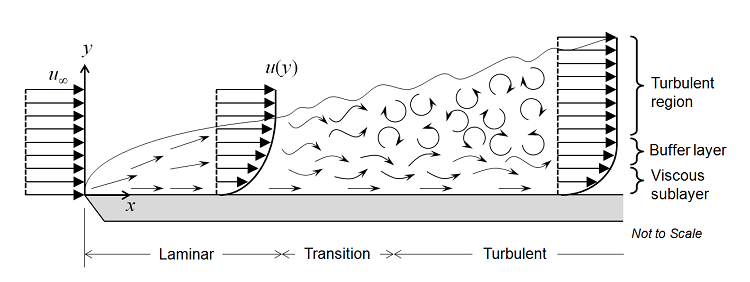
වඩාත් උචිත වඩාත් ගැලපෙන්නේ කුමන ආකාරයේ අනුකෘතිය ද යන්න අවස්ථාව අනුව වෙනස් වේ. (යමක)   යටිතලයෙහි වූ පිළිවෙත් සාර්ථකව අවබෝධ කර  නොගන්නේ නම් හෝ දැන සිටින පිළිවෙත් පිළෛබඳ ගණිතය  සංකීර්ණ නම් භෞතික අනුකෘතියක් වඩාත් යෝග්‍ය විය හැකිය.  තරලවල (fluids ) ආකූල ප්‍රවාහය(turbulent flow) ඒ ආකාර අවස්ථාවක් යයි නිදසුනක් ලෙස  දැක්විය හැකිය. එන්ට එන්ට ම වැඩි වන පරිගණක ආගණනමය වේගය ගණිතමය අනුකෘති කරණය සහ එහි ප්‍රතිඵලයක් වන ග්‍රැෆික් විඩම්බනය ගැටලු වර්ග තව තවත් බොහොමයක් සඳහා යෝග්‍ය බවට පත් කරයි.

මේ ලිපි පෙළ යටතේ ලබන සතියේ නියතතාව සහ විපර්යාසය (CONSTANCY AND CHANGE) ගැන කතා බහ කරමු.

American Association for the Advancement of Science මගින් සකසන Science for All Americans On-Line හි පළවූ  COMMON THEMES  නම්  11 වෙනි පරිචේදය ඇසුරෙන් සැකසෙන ලිපි මාලාවකි,  මේ.